2.3. Sharing Methods
Tip
If you’re having trouble coming up with a design, we recommend you ignore the sharing aspects of the problem first and come up with a design that works for this simplified scenario. After that, you may need to rework some things around to get sharing to work, but it should be simpler to come up with a fully-fledged design once you have a good understanding of how you can implement file confidentiality and integrity on its own.
2.3.1. Sharing semantics
Let \(\mathsf{sender}\) and \(\mathsf{recipient}\) denote two authenticated users, and \(\mathcal{F}\) denote a file uploaded by \(\mathsf{sender}\). \(\mathsf{sender}\) is considered to be the owner of the file.
Sharing operations behave as follows:
\(\mathsf{sender}\) may share \(\mathcal{F}\) with \(\mathsf{recipient}\) by invoking
share_file.In order to access the file, \(\mathsf{recipient}\) must accept \(\mathcal{F}\), by calling
receive_file. After accepting the file, the recipient can access the file usingdownload_file,upload_file,append_file.\(\mathsf{recipient}\)‘s access persists until \(\mathsf{sender}\) revokes \(\mathsf{recipient}\)‘s access to \(\mathcal{F}\) via
revoke_file.That is, you can think of each file as having a set \(\mathcal{S_F}\), denoting the set of users that may access the file. For the purposes of this project, “access” is defined as being able to perform the operations
download_file,upload_file,append_file.Files may be shared with multiple users, but only the file owner may modify sharing: that is, only the owner can share the file with additional users (ie, with
share_file), or remove users withrevoke_file. There is no limit on the number of users who may have access to a file. The owner of a file cannot be changed.All users with whom \(\mathcal{F}\) is shared must have access to the same instance of \(\mathcal{F}\). Thus, any updates made to \(\mathcal{F}\) (such as overwriting via
upload_fileor editing viaappend_file) must be visible to all users with whom the file is shared.Sharing operations MUST NOT require any direct communication between clients. In other words, the only methods of “communication” your client may use to communicate with other users are through the Dataserver and Keyserver.
Specific security requirements for each sharing method are detailed in the individual method specification pages.
2.3.2. Sharing methods
2.3.3. OPTIONAL CS1620/CS2660 Extension: Delegated sharing
Attention
Teams in CS1620/CS2660 may implement either this or
efficient updates using upload_file. Only one extra
requirement is required, even if both students are taking
CS1620/CS2660. This portion is more open-ended than efficient
updates and likely more challenging.
Grading for this part will primarily involve manual review of your code and your design document, rather than autograding. The version of the specification described here is actually quite a restrictive view of sharing. If you choose, you are welcome to make a more featureful version—we’ll be curious to see your design and discuss it with you!
Recipients of a shared file \(\mathcal{F}\) may share \(\mathcal{F}\) with other users, forming a “sharing tree”. For instance, suppose Alice shares \(\mathcal{F}\) with Eleanor and Bob. Bob can then share \(\mathcal{F}\) with Carlos and David, forming the following sharing tree:
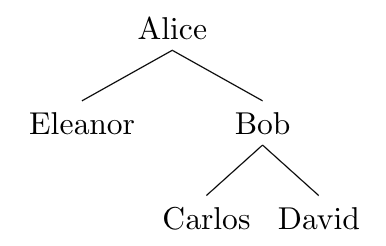
Everyone in the sharing tree for a given file \(\mathcal{F}\)
shares the same instance of \(\mathcal{F}\). Thus, any updates
made to \(\mathcal{F}\) (such as overwriting via
upload_file or editing via append_file)
must be visible to everyone in the tree.
Only the root user in the sharing tree may revoke sharing
permissions (via revoke_file), and they may do so
only on their direct descendants. In the example above, Alice may
revoke Eleanor and Bob’s access to \(\mathcal{F}\), but Alice may
not directly revoke Carlos or David’s access; additionally, even
though Bob shared the file with Carlos and David, Bob may not revoke
Carlos or David’s access. Also, if the root user in the sharing tree
revokes access to one of its direct descendants, the entire subtree
under that child must also lose access. Thus, if Alice revokes Bob’s
access, then Carlos and David must also lose access, and Eleanor’s
access must be unaffected. The client must prevent a revoked user
from taking any action on the file \(\mathcal{F}\) unless an
authorized user shares \(\mathcal{F}\) with that user again.
Calls to revoke_file by anyone in the sharing tree who
is not the root user result in undefined behavior and will not be
tested against your client. Additionally, calls to
revoke_file by the root user where old_recipient
isn’t a direct descendant of the root user in the sharing tree result
in undefined behavior and will not be tested for any particular
behavior.
The behavior of non-tree sharing structures is undefined, and your client will not be tested on such hierarchies. For example, all of the following extensions to the tree above result in undefined behavior, and will not be tested:
David shares \(\mathcal{F}\) with Alice
Eleanor shares \(\mathcal{F}\) with Carlos
Alice shares \(\mathcal{F}\) with David
Alice shares \(\mathcal{F}\) with Bob
While the behavior of the client is unspecified for the aforementioned “undefined” cases (and thus your client may handle such cases in any way it wants), you must make sure to preserve Confidentiality and Integrity even in undefined behavior cases, as the adversary may attempt such actions (or create their own malicious client that attempts similar actions).